|
9. 剛体球流体における相変化の分子動力学シミュレーションによる研究 |
|
A. 研究目標
ガラス状態は工業的に有用な物質状態であり, 現在その応用が期待されている.
しかし, 液体を冷却してガラスに至るガラス遷移現象に関しては未だ理論的に解明されていない.
そこで本研究では, 剛体球系における分子動力学シミュレーションを行い,
ガラス転移点近傍の粒子の振る舞いを明らかにする事を目的とし,
得られたデータを元に理論の構築を目指す.
B. 研究成果
以下にシミュレーション結果を示す.
図1に, 粒子の半径が分散度15%のガウス分布に従う多分散系の平均二乗変位 M2(t) を示す.
長時間スケールで見ると, 体積分率0.580以下の系では平均二乗変位が t に比例しており,
粒子が拡散運動をしていることが確認できる.
また, 体積分率が高くなるにつれて
拡散運動に移行するまでの時間が長くなることが分かる.
一方で, 体積分率0.590以上の場合は, 長時間スケールで見ても t に比例していない.
しかし, 平均二乗変位が増加する徴候を示しており, さらに長時間計算を続けると t に比例することが予想される.
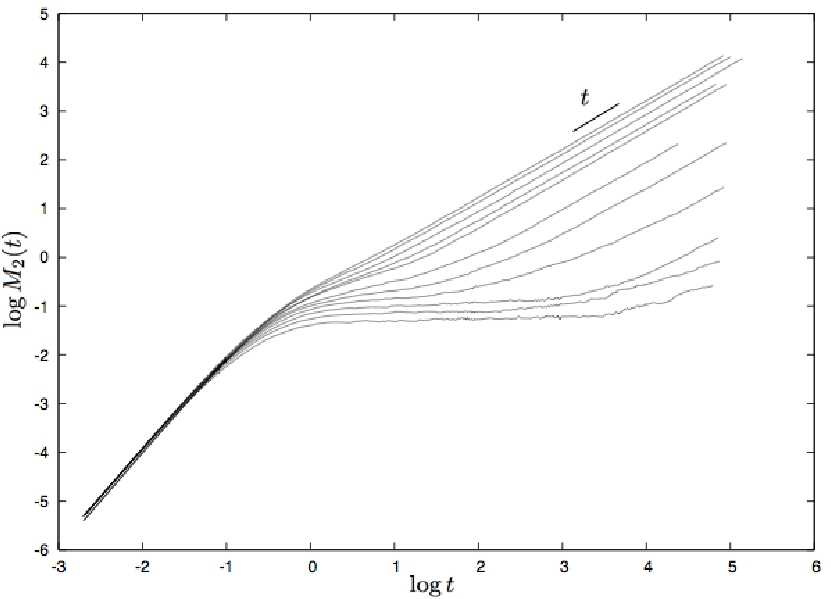
図1:
平均二乗変位の時間変化. 上から体積分率0.500, 0.510, 0.530, 0.550, 0.560,
0.570, 0.580, 0.590, 0.600, 0.610, 0.620の結果を示す.
|
図2に自己中間散乱関数 Fs(t) の時間変化を示す.
体積分率が高くなるにつれて, 自己中間散乱関数が0に収束するまでに時間がかかることが分かる.
体積分率が高い系ほど粒子の動きが遅く初期の構造と相関を持っている時間が長くなるからである.
また, 体積分率が0.550以上になると, はっきりとショルダーが見られる.
これは, 過冷却液体やガラスに見られる特徴であり, 系が単純な液体でないことが分かる.
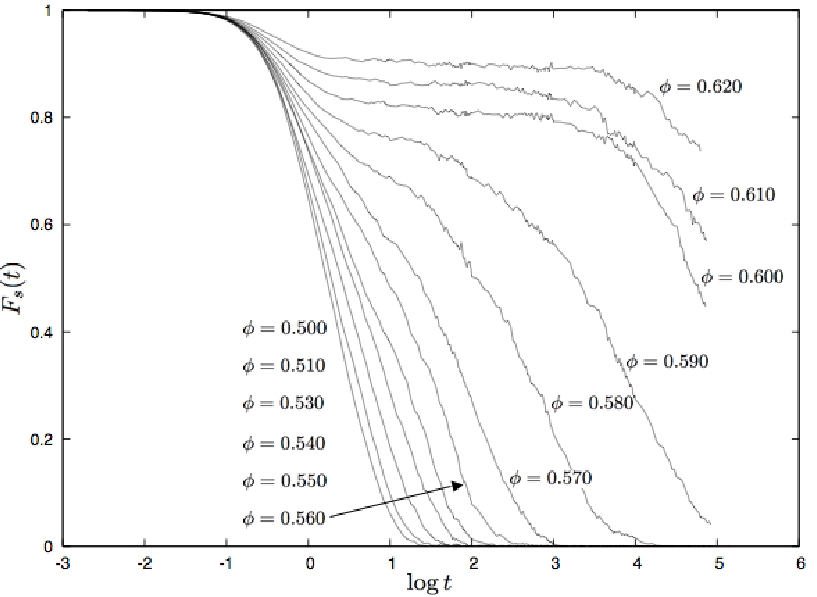
図2:
多分散系の自己中間散乱関数と時間の関係. (波数k = 3.53)
|
図3に, 単分散系と多分散系の圧力の比較を示す.
単分散系では相転移が起こるため体積分率0.507及び0.535で圧力に飛びが見られる.
また, 多分散系でも体積分率0.520および0.540で圧力が飛んでいることが分かる.
二つの系を比較すると, 圧力が変化する体積分率はほぼ同じである.
他の物理量の計算結果から, 多分散系では相転移が起こっているとは言えないが,
その付近の体積分率では系の中で何らかの変化が起こっていると言える.
多分散系でどのような変化が起こっているのか明らかにするためには,
今後の更なる解析が必要である.
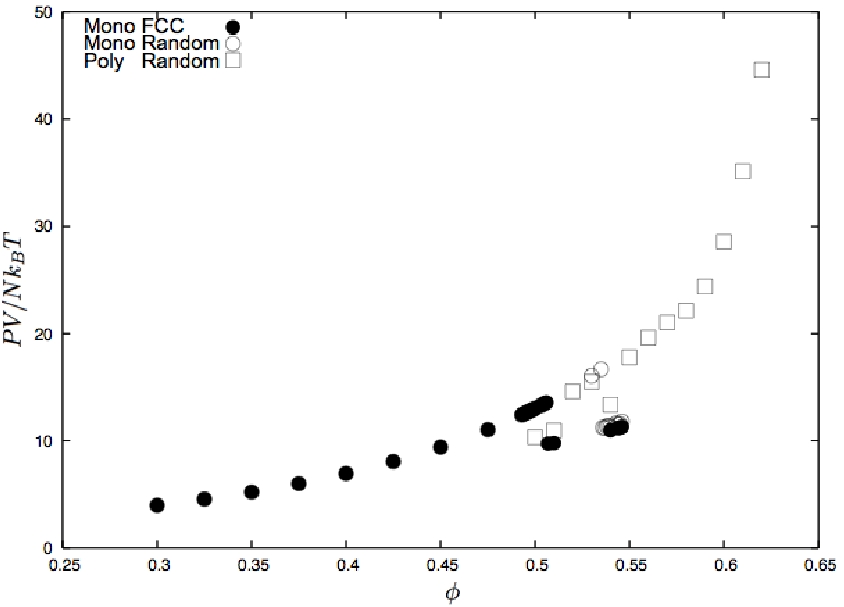
図3:
圧力と体積分率の関係. ● は単分散系の初期配置を面心立方格子とする系, ○ は単分散系の初期配置
をランダム配置とする系, □ は多分散系の初期配置をランダム配置とする系の結果を示す. p は圧力, V は
システムの体積, N は粒子数, kB はボルツマン定数, T は温度を表す.
|
参考文献
-
- 1
-
山崎 裕之,剛体球系における固液相転移現象の計算機実験による研究,
東北大学工学研究科修士学位論文(2003)
- 2
-
小平 絵里, 徳山道夫, 寺田弥生, 東北大学流体科学研究所報告書, 19 (2007).



