ガラス転移点近傍で成立つ分子場理論を紹介する. この理論は次の二種類の体系
(A) コロイド分散系(中性剛体球、荷電コロイド、磁性コロイド等々)
(B) 原子・分子系
に対するデータ解析でも分かるように、過冷却液体のダイナミクスを非常に良く説明し得る. 何故そのような式が成立つのかの本質論は、これからの議論に委ねられるが、あらゆる粘性液体のガラス転移近傍でのダイナミクスを予測出来る発見科学的な意味合いを持つと考えられる.
時刻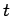 での
での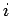 番目の粒子の位置ベクトルを
番目の粒子の位置ベクトルを
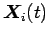 とする. このとき、平均二乗変位
とする. このとき、平均二乗変位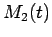 は次のように与えられる.
は次のように与えられる.
![$\displaystyle M_2(t)=\frac{1}{N}\sum_{i=1}^N<[\bm{X}_i(t)-\bm{X}_i(0)]^2>,$](img6.png) |
(1) |
ここで、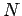 は全粒子数である. 文献 [1]に詳細は譲るとして, 平均二乗変位は次のような平均場方程式に従うことが示される:
は全粒子数である. 文献 [1]に詳細は譲るとして, 平均二乗変位は次のような平均場方程式に従うことが示される:
(A) コロイド分散系
![$\displaystyle \frac{d}{dt}M_2(t)=2dD_S^L(p)+2d\left[D_S^S(p)-D_S^L(p)\right]e^{-M_2(t)/\ell(p)^2},$](img8.png) |
(2) |
(B) 原子・分子系
![$\displaystyle \frac{d}{dt}M_2(t)=2dD_S^L(p)+2d\left[\frac{v_0^2}{d}t-D_S^L(p)\right]e^{-M_2(t)/\ell(p)^2},$](img9.png) |
(3) |
ここで、 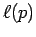 は自由長と呼ばれる長さで、そのスケール程度では粒子間の相互作用が存在しない.
は自由長と呼ばれる長さで、そのスケール程度では粒子間の相互作用が存在しない. 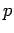 は体系のコントロールパラメータで、
は体系のコントロールパラメータで、
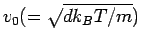 は平均粒子速度、
は平均粒子速度、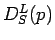 は長時間拡散係数、そして
は長時間拡散係数、そして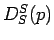 は短時間拡散係数を表す. ここに、
は短時間拡散係数を表す. ここに、 は体系の温度、
は体系の温度、 は粒子の質量である.
は粒子の質量である.
式 (2) 、 (3) は容易に解けて,各系に対してそれぞれ次の解を得ることが出来る.
![$\displaystyle M_2(t)=\ell^2\ln\left[1+\frac{D_S^S}{D_S^L}\left\{e^{2dD_S^Lt/\ell^2}-1\right\}\right],$](img17.png) |
(4) |
![$\displaystyle M_2(t)=\ell^2\ln\left[1+2\left(\frac{\ell v_0}{2dD_S^L}\right)\left\{e^{2dD_S^Lt/\ell^2}-1-2dD_S^Lt/\ell^2\right\}\right].$](img18.png) |
(5) |
文献[1]に示されたように、この解は次の4つの特性時間を持つことが分かる.
| 自由時間 |
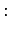 |
 (case (A)) (case (A))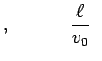 (case (B)) (case (B)) |
|
| プラトウ時間 |
 |
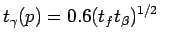 (case (A)) (case (A))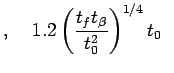 (case (B)) (case (B)) |
|
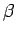 緩和時間 緩和時間 |
 |
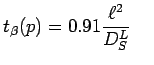 (case (A)) (case (A)) (case (B)) (case (B)) |
|
| 長時間拡散時間 |
 |
 (case (A), (B)) (case (A), (B)) |
(6) |
ここに、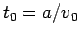 である. 従って、時間発展には次の3つの特性段階が存在する.
である. 従って、時間発展には次の3つの特性段階が存在する.
![$ [E]$](img29.png) 初期段階:
初期段階: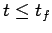
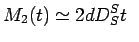 (case (A)) (case (A))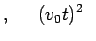 (case(B)) (case(B)) |
(7) |
![$ [\beta]$](img33.png)
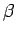 段階:
段階:
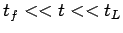
![$ [\beta_f]$](img35.png) 早い
早い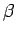 段階:
段階:
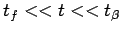
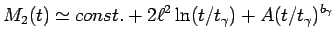 |
(8) |
![$ [\beta_s]$](img38.png) 遅い
遅い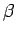 段階:
段階:
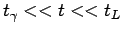
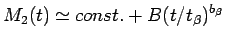 |
(9) |
![$ [L]$](img41.png) 後期段階:
後期段階: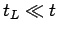
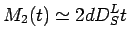 |
(10) |
ここに、指数
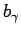 、
、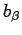 は共に1より大きい値を持ち,特に、コントロールパラメータ
は共に1より大きい値を持ち,特に、コントロールパラメータ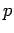 がガラス点移転以上では、
がガラス点移転以上では、
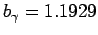 (case(A))、
(case(A))、
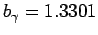 (case(B))となる.
(case(B))となる. 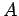 、
、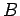 は正の定数である. 重要な結果は、両系において、早い
は正の定数である. 重要な結果は、両系において、早い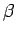 段階では、平均二乗変位は対数増加(
段階では、平均二乗変位は対数増加(
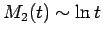 )を示すことである. 散乱関数では、これはlogarithmic decayとなる.
)を示すことである. 散乱関数では、これはlogarithmic decayとなる.
図1において、上記で提案された平均二乗変位の解 (4)はvan Megenら [2]によって得られた中性コロイド実験
のデータと比較される. コントロールパラメータは体積分率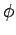 で与えられる.
で与えられる.
図 1:
Comparison between the experimental results and the mean-field results. The red solid lines indicate the experimental results and the blue solid lines the mean-field results.
|
|
図2において、平均二乗変位の解 (5)は、 Tokuyama and Terada [3,4]によって得られた剛体球流体に対するシミュレーション結果と比較される. コントロールパラメータは体積分率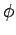 で与えられる.
で与えられる.
図 2:
Comparison between the simulation results for the hard-sphere fluid and the mean-field results. The red solid lines indicate the simulation results and the blue solid lines the mean-field results.
|
|
最後に,図3において、平均二乗変位の解 (5)は、 Gallo, et al [5]らによって求められた、レナード・ジョーンズ系に対するシミュレーションの結果と比較される. コントロールパラメータは温度の逆数 で与えられる.
で与えられる.
図 3:
Comparison between the simulation results for the Lennard-Jones liquids and the mean-field results. The red solid lines indicate the simulation results and the blue solid lines the mean-field results.
|
|
理論と各データとの比較においては、自由長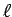 をadjustable parameterとして変化させて、両結果をフィットさせた. その結果は、図4に、コロイド系と剛体球流体系の場合が示されている. 比較の為に、下記で与えられる結晶での自由長
をadjustable parameterとして変化させて、両結果をフィットさせた. その結果は、図4に、コロイド系と剛体球流体系の場合が示されている. 比較の為に、下記で与えられる結晶での自由長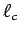 も図示されている.
も図示されている.
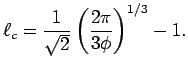 |
(11) |
図 4:
The free length versus the volume fraction. The red circles indicate the experimental results, the blue circles the simulation results, and the green line the free length of crystal.
|
|
また、図5には、 自由体積
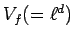 も参考のため示されている.
も参考のため示されている.
図 5:
The free volume versus the volume fraction. The details are the same as in Fig. 4.
|
|
図6では、 コロイド系および剛体球流体系における長時間自己拡散係数
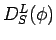 が示されている. 両系に於ける理論線は全く同じ、マスターカーブで表される点に注意のこと(詳細は,文献[1]参照).
が示されている. 両系に於ける理論線は全く同じ、マスターカーブで表される点に注意のこと(詳細は,文献[1]参照).
図 6:
The long-time self-diffusion coefficient versus the volume fraction. The red circles indicate the experimental results and the blue circles the simulation results. The solid lines indicate the non-singular functions of 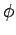 predicted by Tokuyama [1,6]. The difference between coefficients is mainly due to the existence of the long-time hydrodynamic interactions in the experiment [1,3].
predicted by Tokuyama [1,6]. The difference between coefficients is mainly due to the existence of the long-time hydrodynamic interactions in the experiment [1,3].
|
|
分子場理論による、各系のデータ解析により得られた重要な結論は次の点である:
(1) 長時間自己拡散係数
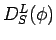 がどの体積分率に対しても特異点を持たない点である. 別の言葉で言えば、ガラス転移点でゼロとはならない.
がどの体積分率に対しても特異点を持たない点である. 別の言葉で言えば、ガラス転移点でゼロとはならない.
(2) あらゆる特性時間がガラス転移点で異常(発散)を示さないと言うことである.
(3) 早い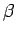 段階では、平均二乗変位は対数増加(散乱関数は対数減少)の漸近解
段階では、平均二乗変位は対数増加(散乱関数は対数減少)の漸近解
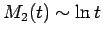 に従う.
に従う.
(4) 遅い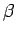 段階では、平均二乗変位は良く知られている、von Schweidler lawではなく、冪乗則
段階では、平均二乗変位は良く知られている、von Schweidler lawではなく、冪乗則
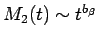
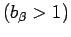 に従う.
に従う.
以上の普遍性は他の系,例えば、磁性コロイド系でも確かめられており、他の様々な系でも同様と予想される. このように、分子場理論は発見科学としての役割を演じるものとして期待される.
- 1
- M. Tokuyama, Physica A, 364, 23-62 (2006).
- 2
- W. van Megen, T. C. Mortensen, S. R. Williams, J. Müller, Phys. Rev. E 58, 6073 (1998).
- 3
- M. Tokuyama, H. Yamazaki, and Y. Terada, Phys. Rev. E 67, 062403 (2003).
- 4
- M. Tokuyama and Y. Terada, J. Phys. Chem. B 109, 21357 (2005); to be published in AIP Conference Series (July, 2006); to be submitted to J. Phys. Condensed Matters (January, 2006).
- 5
- P. Gallo, R. Pellarin, and M. Rovere, Phys. Rev. E 67, 041202 (2003).
- 6
- M. Tokuyama, Physica A 289, 57 (2001).
![]() での
での![]() 番目の粒子の位置ベクトルを
番目の粒子の位置ベクトルを
![]() とする. このとき、平均二乗変位
とする. このとき、平均二乗変位![]() は次のように与えられる.
は次のように与えられる.
 (case (A))
(case (A))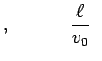 (case (B))
(case (B))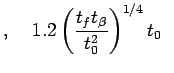 (case (B))
(case (B))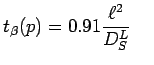 (case (A))
(case (A)) (case (B))
(case (B)) (case (A), (B))
(case (A), (B))![]() で与えられる.
で与えられる.
![\includegraphics[width=140mm]{figA-tokuyama.eps}](img51.png)
![\includegraphics[width=140mm]{figB-tokuyama.eps}](img52.png)
![\includegraphics[width=140mm]{figC-tokuyama.eps}](img54.png)
![]() をadjustable parameterとして変化させて、両結果をフィットさせた. その結果は、図4に、コロイド系と剛体球流体系の場合が示されている. 比較の為に、下記で与えられる結晶での自由長
をadjustable parameterとして変化させて、両結果をフィットさせた. その結果は、図4に、コロイド系と剛体球流体系の場合が示されている. 比較の為に、下記で与えられる結晶での自由長![]() も図示されている.
も図示されている.
![\includegraphics[width=100mm]{figD-tokuyama.eps}](img58.png)
![]() が示されている. 両系に於ける理論線は全く同じ、マスターカーブで表される点に注意のこと(詳細は,文献[1]参照).
が示されている. 両系に於ける理論線は全く同じ、マスターカーブで表される点に注意のこと(詳細は,文献[1]参照).
![\includegraphics[width=100mm]{figF-tokuyama.eps}](img62.png)
![]() がどの体積分率に対しても特異点を持たない点である. 別の言葉で言えば、ガラス転移点でゼロとはならない.
がどの体積分率に対しても特異点を持たない点である. 別の言葉で言えば、ガラス転移点でゼロとはならない.
![]() 段階では、平均二乗変位は対数増加(散乱関数は対数減少)の漸近解
段階では、平均二乗変位は対数増加(散乱関数は対数減少)の漸近解
![]() に従う.
に従う.
![]() 段階では、平均二乗変位は良く知られている、von Schweidler lawではなく、冪乗則
段階では、平均二乗変位は良く知られている、von Schweidler lawではなく、冪乗則
![]()
![]() に従う.
に従う.