ガラス形成物質と異なって、コロイド系ではコントロールパラメータは温度ではなく、コロイド粒子の体積比
上述のような中性コロイド系の局所体積比
1. 過冷却液体とガラス転移の理論的研究
(2) 過冷却液体とガラス転移のダイナミクス |
|
| A. | 研究成果 | B. | 研究目標 |
A. 過冷却液体とガラス転移のダイナミクス
−空間不均一構造の密度揺らぎのダイナミクスに及ぼす影響−
(1) 緒言
ガラスは、文明発祥以来数千年、人類に最も馴染みの深い物質の一つであり、その工学的・工業的有用性は良く知られているところである。液体を高温側から急冷して行くと、結晶化することなく過冷却液体になる。更に冷却して行くとガラス転移を経てアモルファスな固体、即ちガラスになる。熱力学的測定により初めてガラス転移現象が観測されて以来、ほぼ80年の歴史があるがそのメカニズムは未だ謎のままである。最近の科学技術の発達により、液体-ガラス転移のダイナミクスが、実験・計算機実験により精力的に研究されては来ているが、そのメカニズムの理論的解明には程遠く、最も難しい物性・統計物理学の問題のひとつとなっている。 液体-ガラス転移現象は通常のガラス形成物質に限らず、コロイド分散系、高分子系、電磁流体系等々様々な分野に於いて見られる普遍的現象である。ここでは、コロイド分散系を統計物理学観点から研究し、そのメカニズムの解明に挑む。
(2) コロイド分散系
平衡液体中に沢山の中性コロイド粒子を分散させた系を考える。コロイド粒子は、液体粒子からのランダムな力によりそれぞれは独立にブラウン運動を行う。また、コロイド粒子間には、お互いが衝突することによる、直接相互作用と遠くにいても液体を通して時間と共に相互作用し合う、流体力学的相互作用が働いている。ガラス転移点近傍では、多体相関の結果として、流体集団協同運動が特に重要な役割を演じると考えられる。
ガラス形成物質と異なって、コロイド系ではコントロールパラメータは温度ではなく、コロイド粒子の体積比![]() (=コロイド粒子の全体積
(=コロイド粒子の全体積![]() /体系の全体積
/体系の全体積![]() )である。ここに
)である。ここに![]() はコロイド粒子の半径であり、
はコロイド粒子の半径であり、![]() は全粒子数である。液体の温度・圧力は一定に保った下で、
は全粒子数である。液体の温度・圧力は一定に保った下で、![]() を増加させると、融解体積比
を増加させると、融解体積比![]() 以上で過冷却コロイド液体になり、更に増加させると、ガラス転移体積比
以上で過冷却コロイド液体になり、更に増加させると、ガラス転移体積比![]() 以上でコロイドガラスになることが知られている。普通のコロイド液体状態と過冷却コロイド液体状態との大きな違いは、各粒子の自己拡散係数が後者では前者に比べて非常に小さくなり、コロイド粒子の運動が体積比が増すに従ってよりゆっくりとなることにある。一方ガラス状態では、最大観測時間内に於いてさえ、粒子の運動がほとんど凍りついたようになる。ガラス形成物質では、ガラス転移点近傍で粘性係数が異常に増加し、過冷却状態およびガラス状態が実現される。このように、コロイド系の振舞いはガラス形成物質のそれと定性的に全く似通っている。
以上でコロイドガラスになることが知られている。普通のコロイド液体状態と過冷却コロイド液体状態との大きな違いは、各粒子の自己拡散係数が後者では前者に比べて非常に小さくなり、コロイド粒子の運動が体積比が増すに従ってよりゆっくりとなることにある。一方ガラス状態では、最大観測時間内に於いてさえ、粒子の運動がほとんど凍りついたようになる。ガラス形成物質では、ガラス転移点近傍で粘性係数が異常に増加し、過冷却状態およびガラス状態が実現される。このように、コロイド系の振舞いはガラス形成物質のそれと定性的に全く似通っている。
上述のような中性コロイド系の局所体積比![]() に対して、最近、徳山は次のような非線形拡散確率方程式を提案した[1]。
に対して、最近、徳山は次のような非線形拡散確率方程式を提案した[1]。
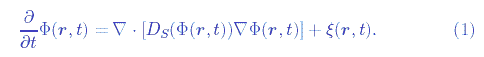
ここで![]() は境界条件
は境界条件![]() を満足するものとする。
を満足するものとする。![]() は、自己拡散係数であり、
は、自己拡散係数であり、![]() の与えられた関数である。
の与えられた関数である。![]() は、ガウス型のホワイトノイズで記述される揺動力である。局所体積比
は、ガウス型のホワイトノイズで記述される揺動力である。局所体積比![]() は平均値
は平均値![]() と揺らぎ
と揺らぎ![]() に分離できる;
に分離できる;![]()
![]() 。これは、ガラス転移が臨界現象とは異なり、ガラス転移近傍に於いてさえ揺らぎの大きさが平均値に比べて小さい為である。即ち、
。これは、ガラス転移が臨界現象とは異なり、ガラス転移近傍に於いてさえ揺らぎの大きさが平均値に比べて小さい為である。即ち、![]() 。このとき、
。このとき、![]() は平均粒子密度の空間的不均一構造の時間発展を記述し、
は平均粒子密度の空間的不均一構造の時間発展を記述し、![]() は平均運動のまわりの粒子密度の揺らぎの時間発展を記述する。実験的には、揺らぎは自己散乱関数
は平均運動のまわりの粒子密度の揺らぎの時間発展を記述する。実験的には、揺らぎは自己散乱関数![]()
![]() を通して観測される。
を通して観測される。
ここでは、式(1)をガラス転移点近傍で、平衡系![]() および非平衡系
および非平衡系![]() において別々に数値計算した、その数値解の結果を以下に報告する。
において別々に数値計算した、その数値解の結果を以下に報告する。
(3) 非平衡系
非平衡系では、平均値![]() が時間・空間において変化している。ここで
が時間・空間において変化している。ここで![]() であるので、式(1)より平均値
であるので、式(1)より平均値![]() および揺らぎ
および揺らぎ![]() に対してそれぞれ次のような方程式が求められる。
に対してそれぞれ次のような方程式が求められる。
非線形確定方程式:
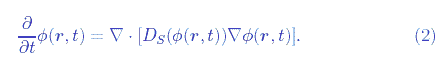
線形確率方程式:

式(3)より、拡散係数![]() の
の![]() 依存性を通して、揺らぎの運動は時間的および空間的に影響されることが分る。初期に平衡から20%空間的に非平衡である系の過冷却液体
依存性を通して、揺らぎの運動は時間的および空間的に影響されることが分る。初期に平衡から20%空間的に非平衡である系の過冷却液体![]() での数値結果を示す。図1は、各特性時間に於ける平均密度
での数値結果を示す。図1は、各特性時間に於ける平均密度![]() のスナップショットを示している[3]。赤で色分けされた部分は、ガラス領域
のスナップショットを示している[3]。赤で色分けされた部分は、ガラス領域![]() を表し、白い部分は液体状態である。ガラス領域の示す不均一構造は長時間存続し、時間スケールによってその形状はそれぞれ異なっている。
を表し、白い部分は液体状態である。ガラス領域の示す不均一構造は長時間存続し、時間スケールによってその形状はそれぞれ異なっている。
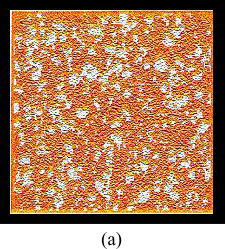
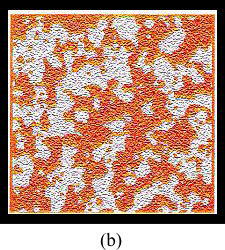



表1に示されるように、時間発展は四つの段階に分けられる。時間毎の異なる空間構造に従って、密度揺らぎも影響を受け、それぞれ異なった漸近緩和関数に従うことが分る。ここで![]() 、
、![]() はそれぞれ短時間および長時間自己拡散係数を表す。
はそれぞれ短時間および長時間自己拡散係数を表す。

(4) 平衡系
平衡系では![]() であるので、式(1)より次のような、3次の非線形確率方程式が求められる
[4] 。
であるので、式(1)より次のような、3次の非線形確率方程式が求められる
[4] 。

ここで係数![]() および
および![]() は
は![]() の既知の関数である。初期に空間的に平衡である系の数値結果を示す[4]。図2(a)は、ある時間に於ける密度揺らぎ
の既知の関数である。初期に空間的に平衡である系の数値結果を示す[4]。図2(a)は、ある時間に於ける密度揺らぎ![]() の過冷却状態(
の過冷却状態(![]() = 0.5704)でのスナップショットを示し、図2(b)は液体状態(
= 0.5704)でのスナップショットを示し、図2(b)は液体状態(![]() = 0.502)でのスナップショットを示している。赤で色分けされた部分は、ガラス領域を表し、緑の部分は過冷却液体領域そして水色の部分は液体領域である。液体状態では、空間不均一構造はほとんどランダムである。一方、過冷却状態では、ガラス領域の示す大きな不均一構造は長時間存続し、時間スケールによってその定性的形状は変化しないように見える
[5, 6] 。
= 0.502)でのスナップショットを示している。赤で色分けされた部分は、ガラス領域を表し、緑の部分は過冷却液体領域そして水色の部分は液体領域である。液体状態では、空間不均一構造はほとんどランダムである。一方、過冷却状態では、ガラス領域の示す大きな不均一構造は長時間存続し、時間スケールによってその定性的形状は変化しないように見える
[5, 6] 。
| (a)過冷却コロイド液体 | ||||
| (1) | (2) | |||
 |
 |
 |
||
|
(1)ガラス転移近傍での密度揺らぎ分布の断面図と (2)ガラス状態の密度揺らぎの分布 (赤:ガラス状態 |
||||
| (b)コロイド液体 | ||||
| (1) | (2) | |||
 |
 |
 |
||
|
(1)ガラス転移から離れたところでの密度揺らぎ分布の断面図と (2)ガラス状態の密度揺らぎの分布 ガラス転移点近傍ではガラス状態のクラスターが大きくなっていることがわかる。 |
||||
| 図2 平衡系でのガラス状態の典型的な配置のスナップショット。 |
表2に示されるように、時間発展は四つの段階に分けられる。時間毎の異なる空間構造に従って、密度揺らぎも影響されてそれぞれ異なった漸近緩和関数に従うことが分る。

(5) 実験との比較
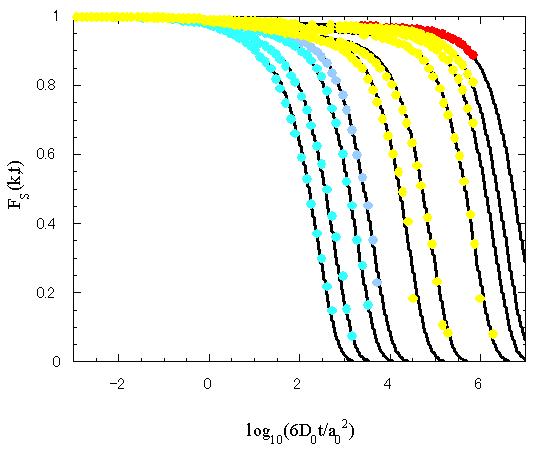
最近のvan Megenグループ[7] による、平衡系に於いてなされた実験結果とここでの数値解の結果とを比較する。図3には、平衡系に於ける散乱関数![]() の時間発展が無次元時間
の時間発展が無次元時間![]() に対してプロットされている。実線が理論値であり、丸印が実験値を表す。比較の為に、非平衡系での理論値を点線で表す。
に対してプロットされている。実線が理論値であり、丸印が実験値を表す。比較の為に、非平衡系での理論値を点線で表す。![]() は一個の粒子の自由拡散係数である。
は一個の粒子の自由拡散係数である。

(6) 結言
図3および表1、2の漸近解から明らかなように、非平衡系の方が2段階緩和過程が平衡系よりはっきりしている。原因は、非平衡系の![]() 緩和過程に於いて見られた小さなクラスターが平衡系に於いては認識できないことに依る。平衡系では、ガラス領域の空間構造が非線形揺らぎそのものによって励起され、小さいクラスター構造は揺らぎそのものに依って容易に壊されると考えられる。一方、非平衡系では、クラスタ−構造そのものは、揺らぎではなく、平均運動として非線形確定方程式により形成され、小さな揺らぎに対しても安定である。このようにして、平衡系では、
緩和過程に於いて見られた小さなクラスターが平衡系に於いては認識できないことに依る。平衡系では、ガラス領域の空間構造が非線形揺らぎそのものによって励起され、小さいクラスター構造は揺らぎそのものに依って容易に壊されると考えられる。一方、非平衡系では、クラスタ−構造そのものは、揺らぎではなく、平均運動として非線形確定方程式により形成され、小さな揺らぎに対しても安定である。このようにして、平衡系では、![]() 緩和過程が弱められる傾向を示す。これは、図3に見られるように理論と実験との一致からも確かめられる。
緩和過程が弱められる傾向を示す。これは、図3に見られるように理論と実験との一致からも確かめられる。
非平衡系での実験はスタートしたばかりであり、その結果と比較する為に、新たなパラメータ値の条件下で式(1)の数値解を求めることが当面の課題である。長期的には、平衡系および非平衡系での数値解と実験との比較を通して、式(1)の正当性を確かめ、その第一原理からの導出を行い、このようにして得られた新しい観点から、ガラス形成物質に於けるガラス転移現象を理解することが最大の課題である。
(7)平衡系でのガラス状態の典型的な配置の時間発展のアニメーション(Link)
参考文献
[1] Michio Tokuyama, Physica A 294, 23-43 (2001).
[2] Michio Tokuyama, Physica A 289, 57-85 (2001).
[3] Michio Tokuyama, Yoshihisa Enomoto, and Irwin Oppenheim, Physica A 270, 380-402 (1999).
[4] Michio Tokuyama, Yayoi Terada, and Irwin Oppenheim, Physica A 307, 27-40 (2002).
[5] Michio Tokuyama, Yayoi Terada, and Irwin Oppenheim, EPJ E 9, 271-275 (2002).
[6] Michio Tokuyama, Yayoi Terada, and Irwin Oppenheim, Physica A 321, 193-206 (2003).
[7] W. van Megen, T. C. Mortensen, S. R. Williams, and J. Müler, Phys.
Rev. E 58, 6073-6085 (1998).
平衡系
これまで、数値的に揺動力の取り扱いが難しいため、揺動力の場所依存性を簡単化したモデルの数値計算を行い、過冷却状態と液体状態は空間構造が異なることを定性的に調べた。そこで、短期目標として、計算が可能なモデルで、より近似の少ないモデルの構築と計算を行い、得られた結果から定量的な解析を行い実験との比較を行うことにより、
ガラス転移点近傍での平衡系での緩和過程の詳細の解明を行う。特に、近似が少ないモデルの計算により、これまでほとんど成功していない定量的な研究を試み、コロイド分散系でのガラス転移現象を理解する。
文責:徳山 道夫、寺田 弥生
| 戻る | 目次 | 進む |