| 3. 非平衡過冷却液体のダイナミクス |
|
| A. | 研究目標 | B. | 研究成果 |
ガラス状態は、自然界や工業技術など至る所で応用されている。粘性液体における液体-ガラス転移の問題は、物性物理に残された最後のフロンティアの一つであるが、未だそのメカニズムの解明に至っていない。しかし、転移点近傍でのダイナミクスの異常は空間構造の変化によることが、最近、実験や理論から解明されつつある。また、計算機の高速化に伴って計算機実験でも空間構造とダイナミクスの関係が研究されている。ガラス状態は粘性液体を急冷することにより得られるが、複雑液体の一つ、コロイド液体もコロイドの密度を増加させると、ある密度でガラス転移を起こすことが実験で確かめられている。ここでは、非平衡コロイド液体に対して提案された、非線形Tokuyama-Oppenheim拡散方程式[1,2]を数値計算し、ガラス転移点近傍の過冷却液体領域では空間構造の時間的変化がどのように密度揺らぎのダイナミクスに影響を与えるかを調べ、液体-ガラス転移のメカニズムを探ることが主目的である。
非線形Tokuyama-Oppenheim拡散方程式は次のように与えられる。
![]()
ここで、![]() は
は![]() を満たす。
を満たす。![]() は平衡体積比、
は平衡体積比、![]() は拡散係数である。
は拡散係数である。
現在の課題
参考文献
[1] Michio Tokuyama and Irwin Oppenheim, Phys. Rev. E 50, R 16-19 (1994).
[2] Michio Tokuyama and Irwin Oppenheim, Physica A 216, 85-119 (1995).
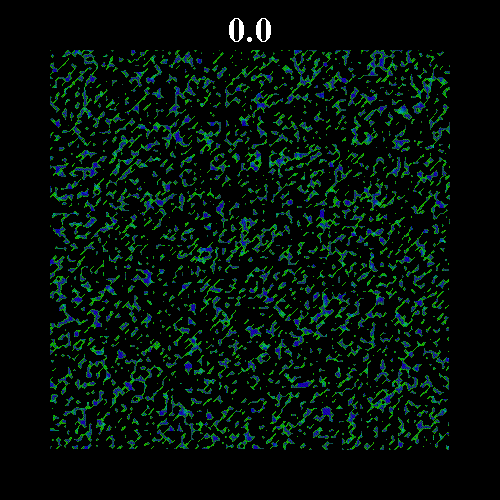
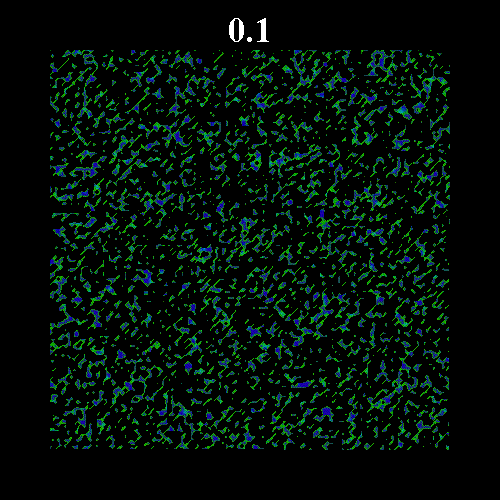
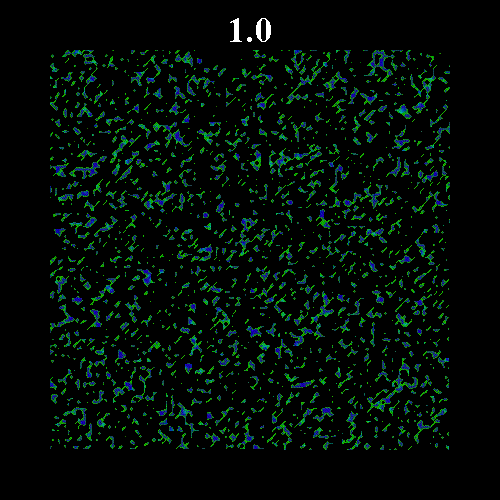
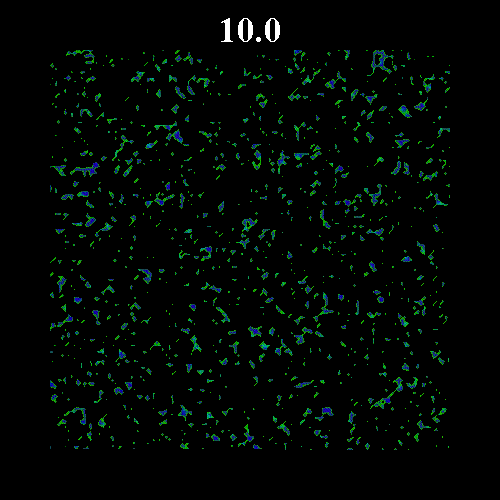
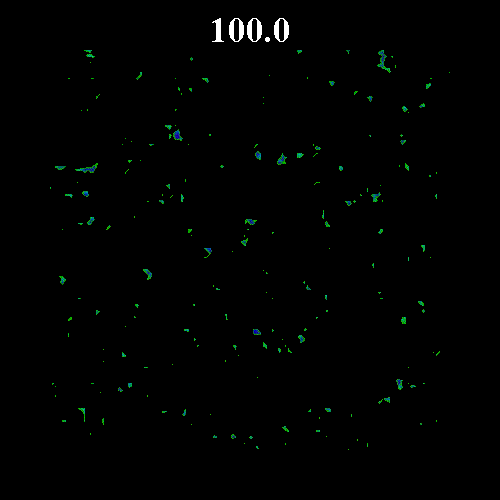
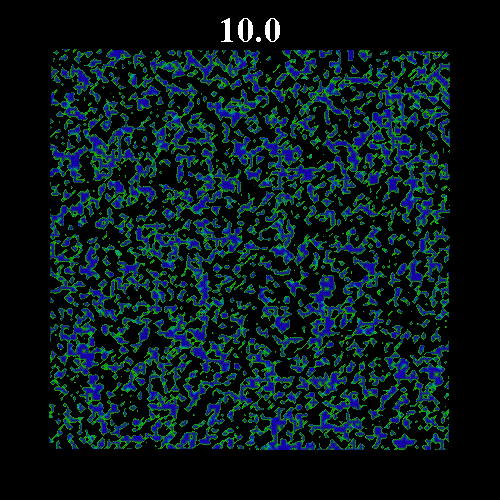
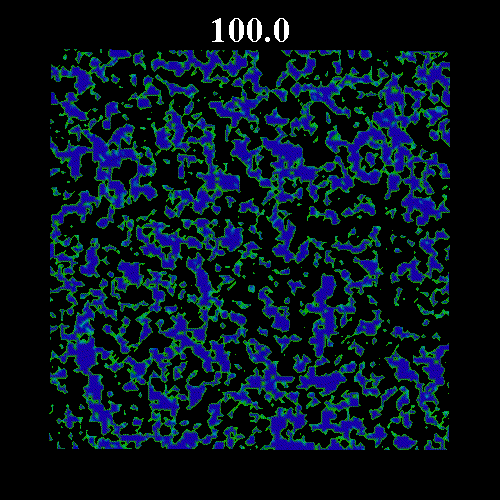
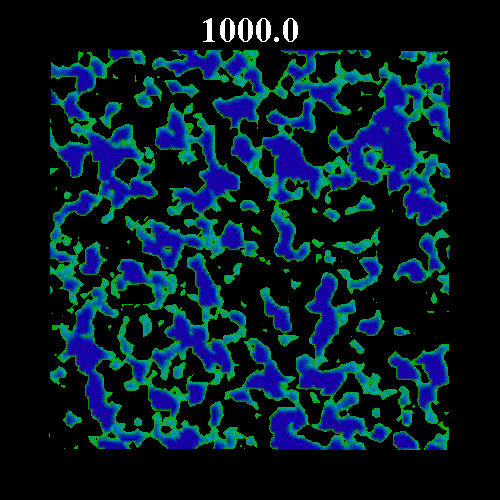
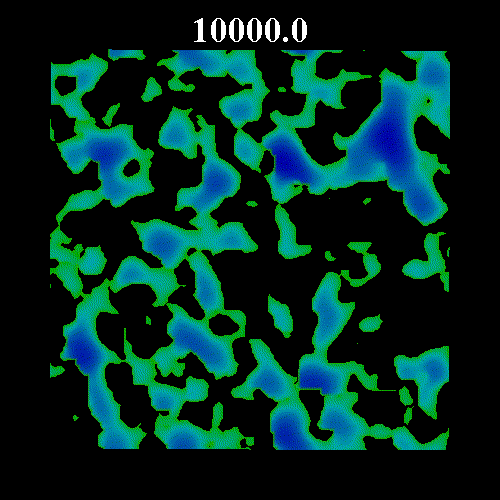
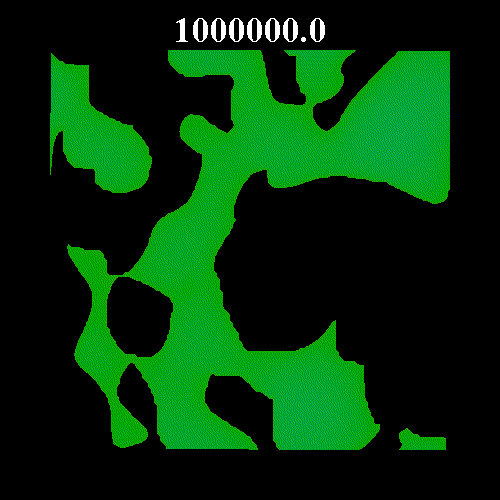
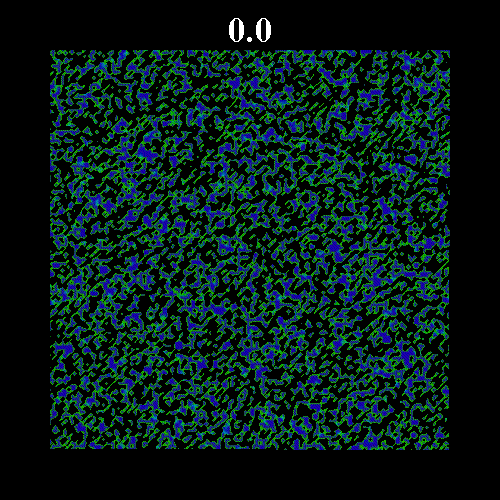
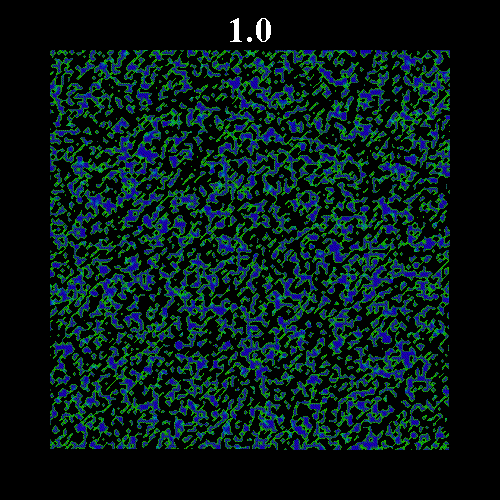
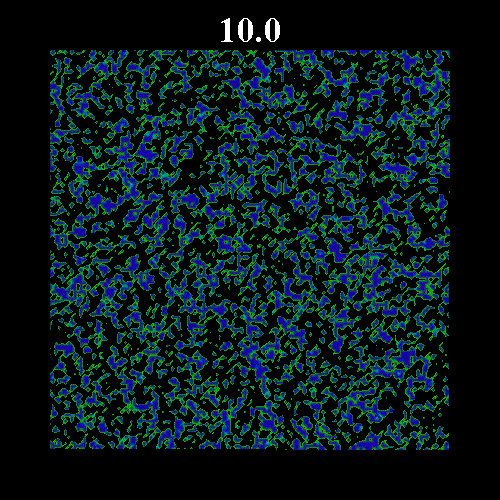
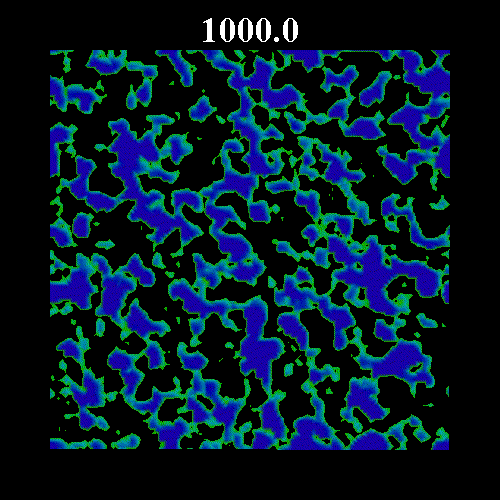
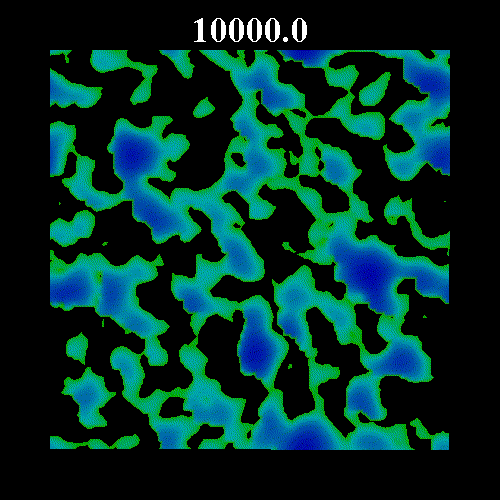
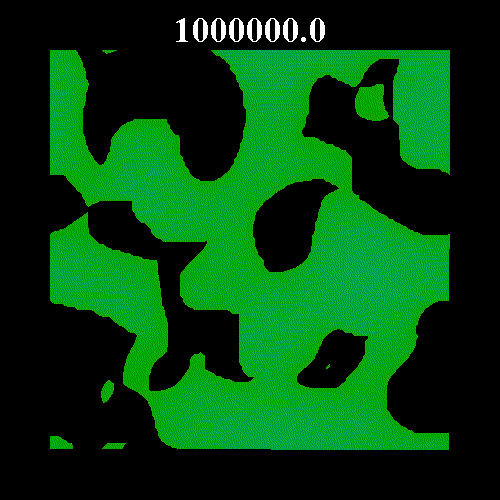
![]() の値を変化させた時のガラス領域のスナップショットを示す。図中の黒い部分は液体領域、緑・青の部分はガラス領域(緑はガラス転移体積比近傍のガラス領域で、青になるほどガラス転移体積比から離れる)を表している。図上部は時刻を表している。いずれも
の値を変化させた時のガラス領域のスナップショットを示す。図中の黒い部分は液体領域、緑・青の部分はガラス領域(緑はガラス転移体積比近傍のガラス領域で、青になるほどガラス転移体積比から離れる)を表している。図上部は時刻を表している。いずれも![]() =0.8 である。なお、
=0.8 である。なお、![]() は次のように表すことのできる平衡度を示している。
は次のように表すことのできる平衡度を示している。
![]()
それぞれの図は、平衡体積比がガラス転移体積比![]() =0.57184 から離れている場合(図1
=0.57184 から離れている場合(図1 ![]() =0.502)と
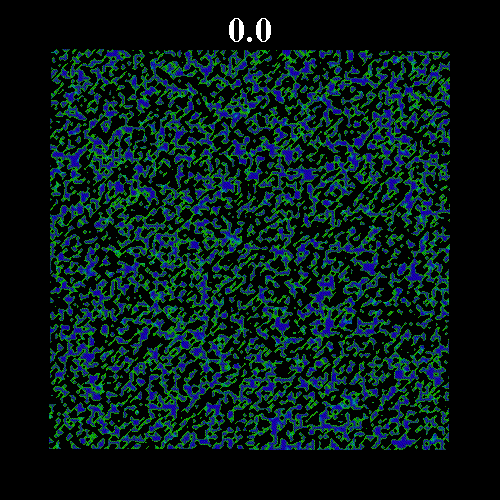
=0.502)と![]() に近い場合(図2
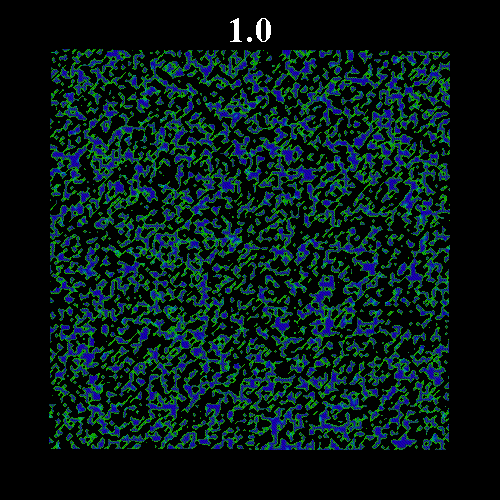
に近い場合(図2 ![]() =0.571, 図3
=0.571, 図3 ![]() =0.573)を示している。図2・3にみられるように平衡体積比がガラス転移体積比に近い場合、ガラス領域の固まりが形成され非常にゆっくりとした緩和となっている。
=0.573)を示している。図2・3にみられるように平衡体積比がガラス転移体積比に近い場合、ガラス領域の固まりが形成され非常にゆっくりとした緩和となっている。
 |
 |
 |
 |
 |
 |
| 図1 | ||
 |
 |
 |
 |
 |
 |
 |
 |
|
| 図2 | ||
 |
 |
 |
 |
 |
 |
 |
 |
|
| 図3 | ||
文責:志村 努
| 戻る | 目次 | 進む |