Theoretical Fluid Dynamics Laboratory

4.　レナードジョーンズ流体における
過冷却液体とガラスの研究

A.　研究目標

ガラスは人類とは切っても切れない関係にある．今から5000年ほど前に偶然にして初めて精製されたとされるガラスは長い時を経た今でも重要な材料として用いられている[1]．

通常，液体を融点以下の温度に冷却すると結晶となる．しかし，急冷や混合といった特殊な条件により結晶化を避けつつ冷却すれば（準）安定状態である過冷却液体に，さらに冷却するとガラスとなる．ここでいうガラスとは，粘性が非常に強いためにほとんど流動していないように見える流体の総称であり，材料の１つとして日常生活で用いられている概念とは異なる．なお，工学的には粘性率が10の13乗ポワズを超える流体をガラスと定義している．室温におけるマヨネーズの粘性率が10ポワズ程度であることを考えると，ガラスは実用的な時間スケールでは固体として扱えるくらいに粘性の大きい流体である．しかしながら，実際は長い時間をかけて流動している．

ガラス物性の工学的研究が非常に進んでいるのに対して，ガラス転移メカニズムやスローダイナミクス（過冷却液体からガラスへと至る際に粘性率が飛躍的に増大する現象）の起源についての理論的解明は未だ完全にはなされていない．近年は大規模なシミュレーションも行われており，これまでになされた膨大な実験データと合わせて，理論的解明に向けての気運が高まっている[2]．ガラスや過冷却液体の更なる応用の可能性のためにも，転移メカニズムやスローダイナミクスの起源の解明は必要不可欠であろう．

最終的な目標は，ガラス転移メカニズムとスローダイナミクスの起源の解明である．そのような最終目標を念頭に置きつつ，レナードジョーンズポテンシャルによって粒子同士の二体相互作用が記述される系を平均場理論（MFT）[3, 参照HP]によって解析することで，過冷却液体やガラスについての理解を深めることを目標とする．本研究では１種類の粒子からなる系と２種類の粒子からなる系を比較することで，同じ相互作用に支配されるシステムについての普遍性の存在を確かめ，さらに長時間拡散係数がガラスや過冷却液体の系を記述するコントロールパラメターとして適しているという主張[4]をレナードジョーンズ系について確かめた．なお，システムの詳細については参考文献[5]を参照していただきたい．

B.　研究成果

　(1)長時間自己拡散係数

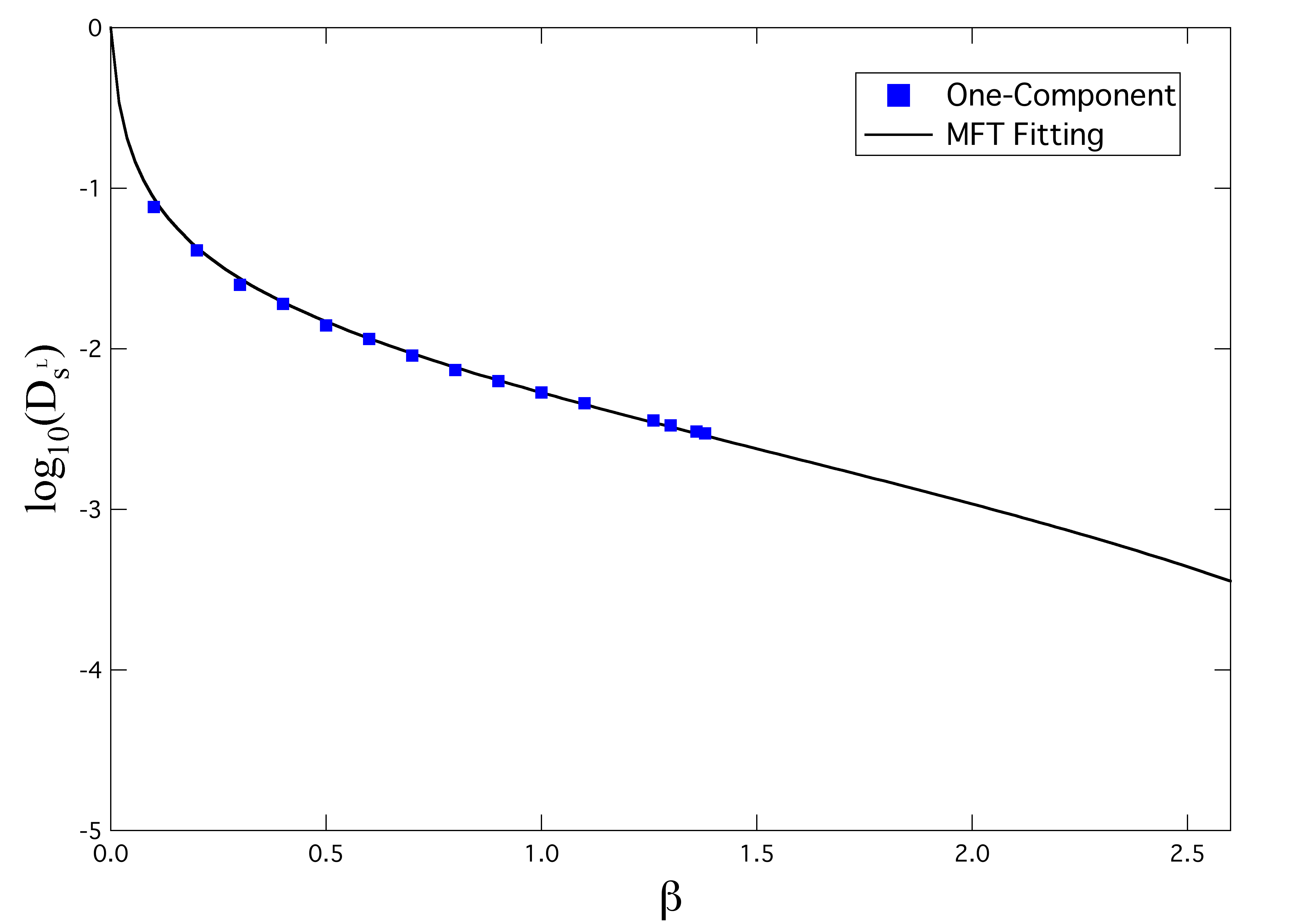
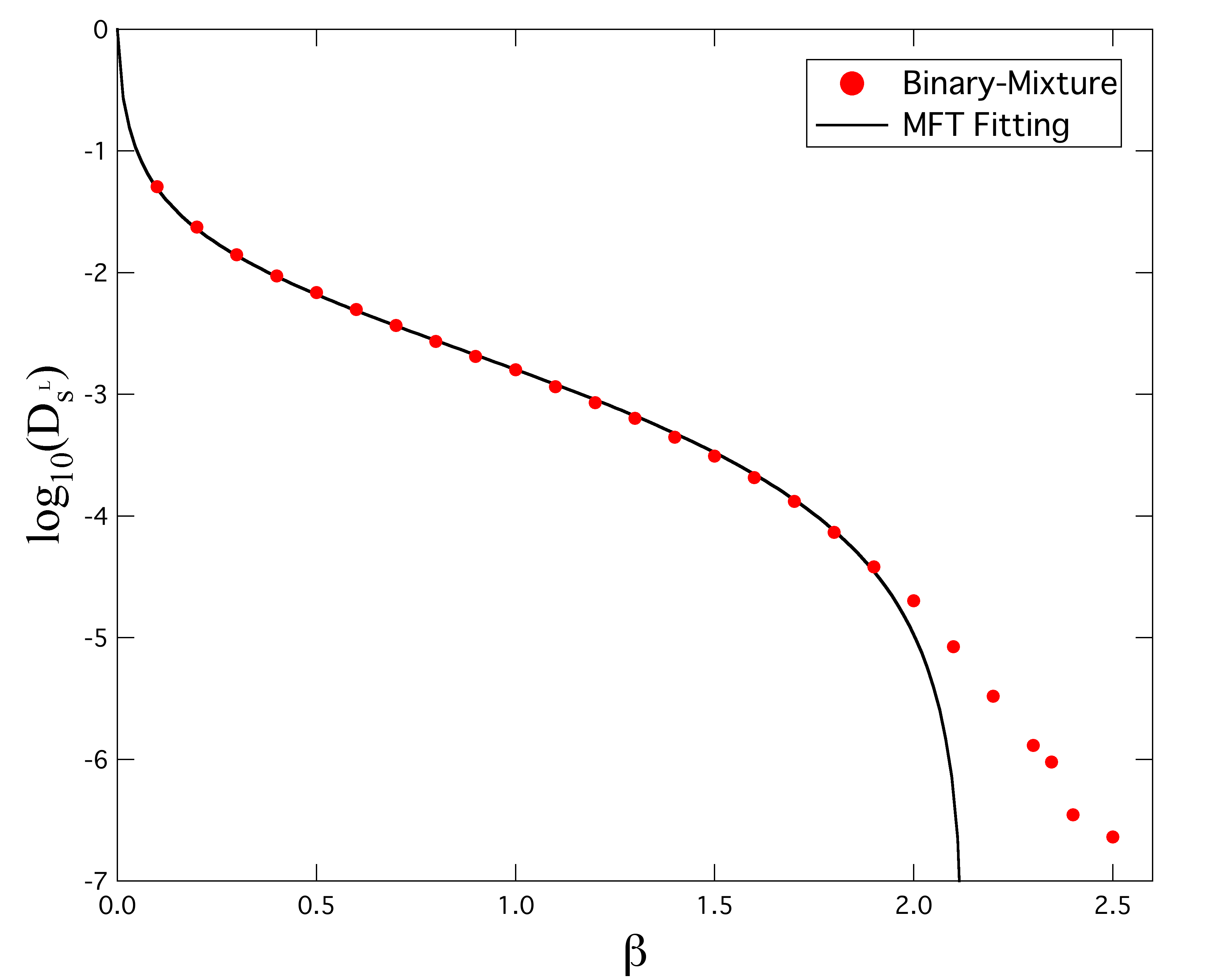
図1と図2に１成分系と２成分系における無次元化された長時間自己拡散係数の結果を示す．横軸は無次元化された逆温度であり，実線は平均場理論（MFT）によるフィッティングを表す．１成分系では結晶化が起こるために無次元化温度で0.724以下（逆温度で1.38以上）では長時間自己拡散係数は測定できないが，２成分系では２種類を混合しているために低温でも結晶にはならず長時間自己拡散係数の測定が可能である．

**図1:**１成分系における長時間拡散係数

**図2:**２成分系における長時間拡散係数

１成分系も２成分系も高温領域では平均場理論はシミュレーション結果と良い一致を見せている．しかしながら，２成分系での低温領域ではシミュレーション結果は平均場理論とは合わない．これは，過冷却液体からガラスへの転移が相転移ではなく動的な遷移である可能性があるのだが，理論的に扱う際に特異的な温度の存在を仮定しているためにおこるものである．なお，徳山はこの特異的な長時間自己拡散係数の式から非特異的な長時間自己拡散係数の式へと変換する方法も提案している[6]のだが，ここでは普遍性について調べるので特異的な長時間自己拡散係数の式によるフィッティングで十分である．

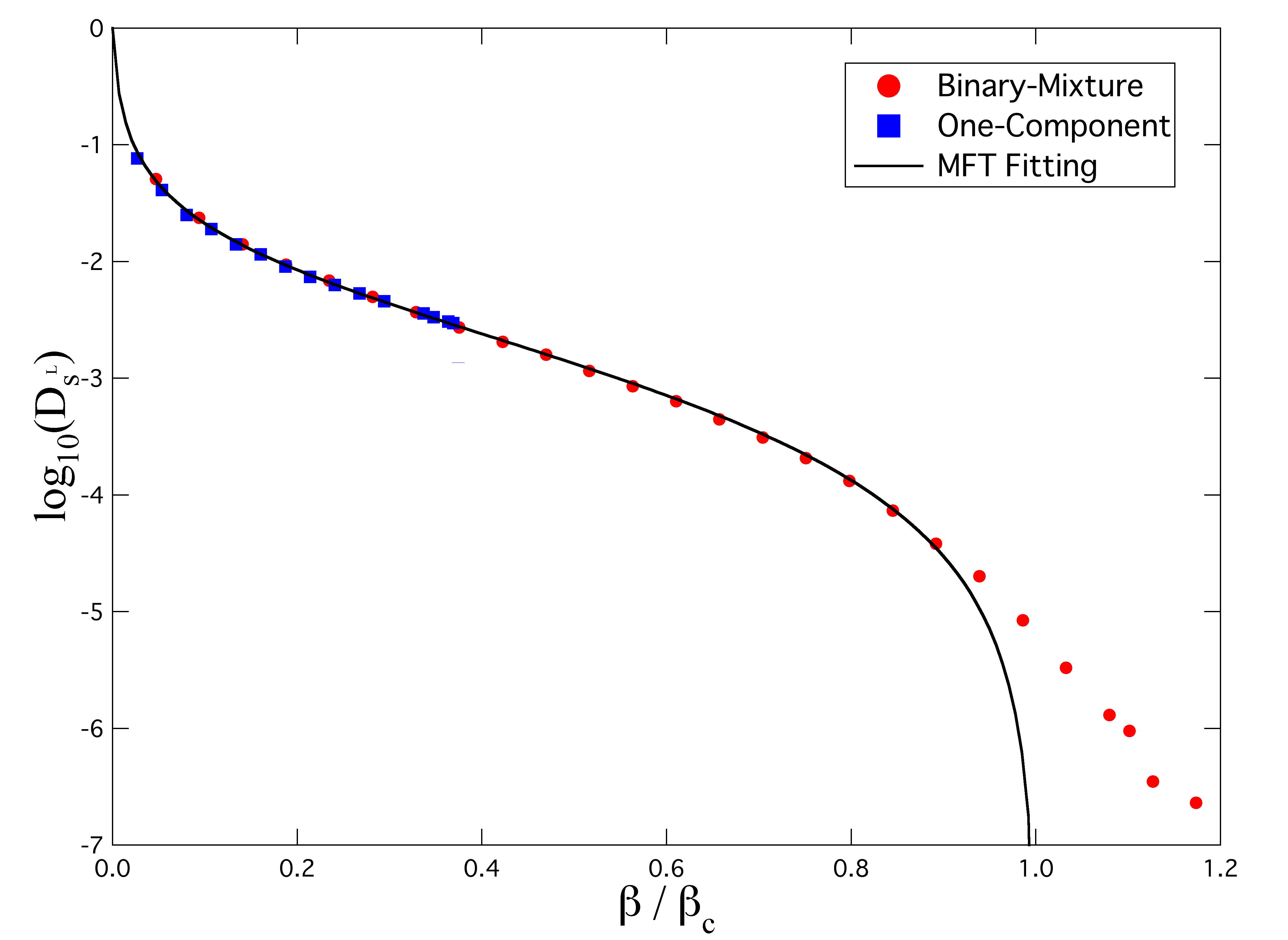
さて，特異的な長時間自己拡散係数の式では特異逆温度βcとパラメータKによりフィッティングを行うのだが，それらの値は，１成分系ではK=374，βc=3.74であり，２成分系ではK=374，βc=2.13である．このように，相互作用が同じ系では粒子の混合比や数密度が異なっていてもパラメータKの値は等しくなり，システムの詳細な情報は特異逆温度βcが担うこととなる．図3に横軸を特異逆温度によって規格化された逆温度としたときの長時間自己拡散係数の振る舞いを示す．システムの詳細を含むβcにより規格化したことで１つのマスターカーブで長時間自己拡散係数の振る舞いが記述できている．このように，同じ相互作用により記述できる系には普遍性が存在することが確認された．なお，この普遍性はGalloらによって行われた同じくレナードジョーンズポテンシャルによって相互作用が記述されるシミュレーションモデル[7]についても確かめられている．

**図3:** βcにより規格化された逆温度と長時間自己拡散係数の関係

　(2)平均自由行程

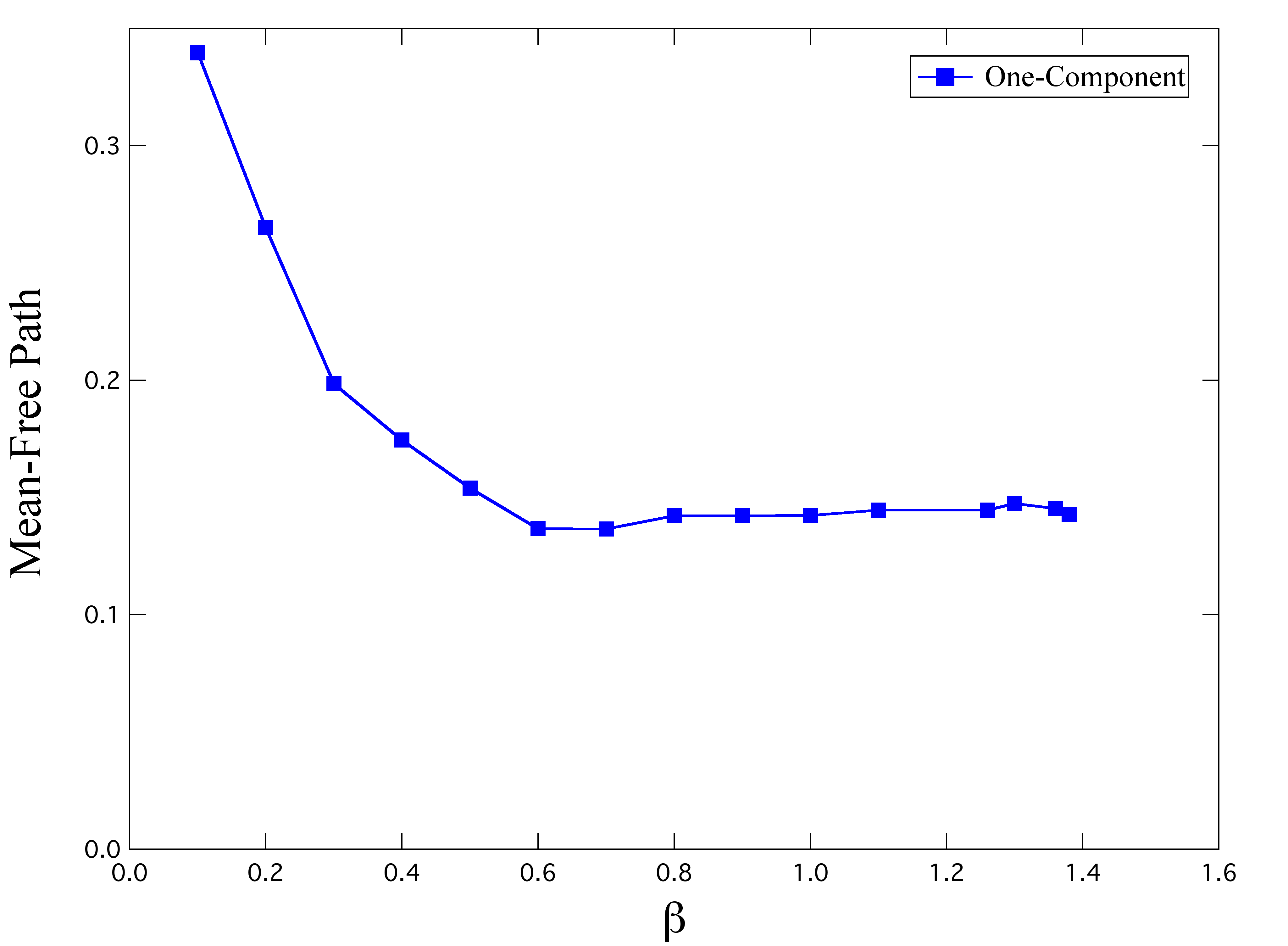
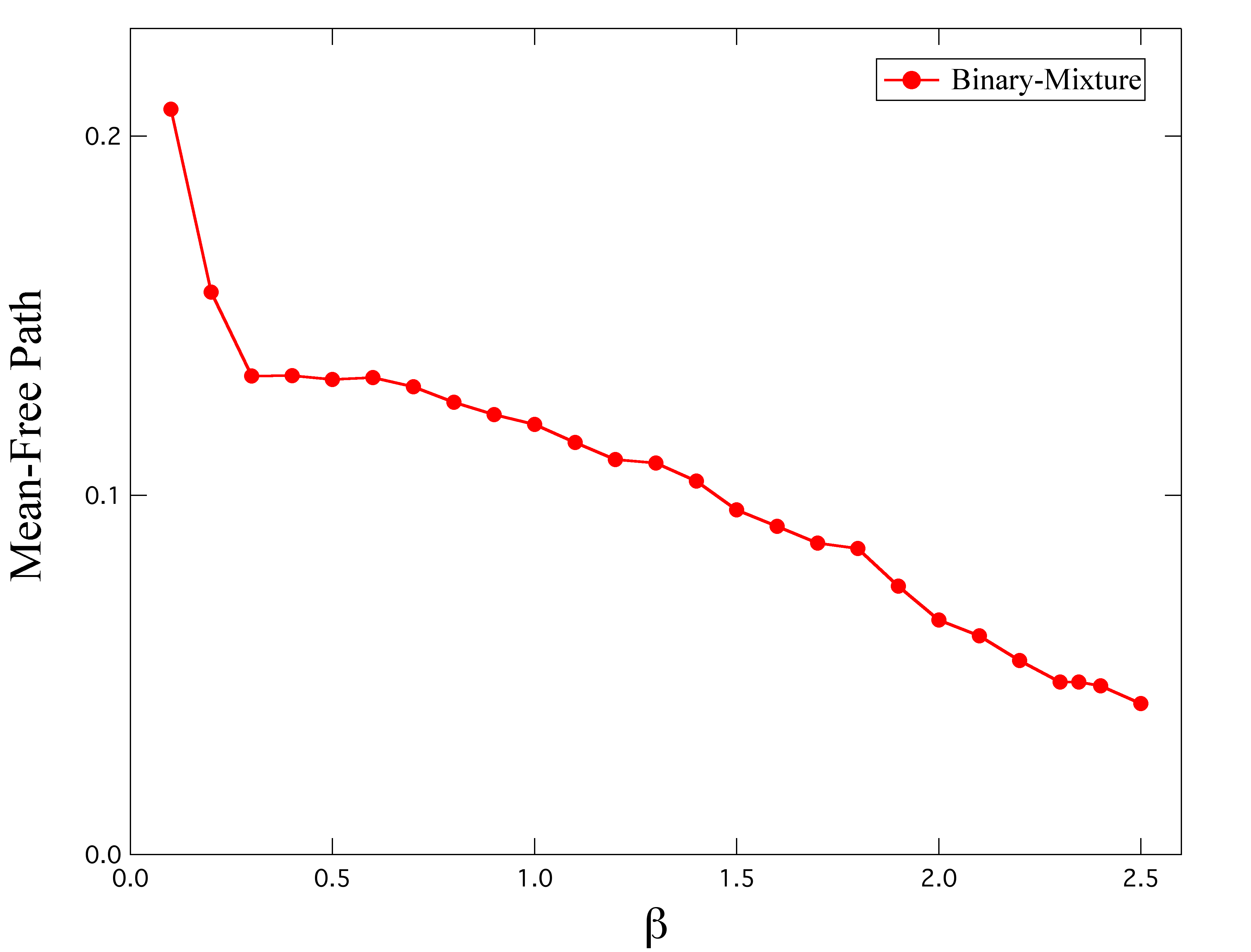
前セクションにおいて，長時間自己拡散係数を平均場理論により解析した．平均場理論は平均二乗変位の振る舞いも記述する．その際にパラメータとなるのが長時間自己拡散係数と平均自由行程と呼ばれる量である．平均自由行程は粒子が相互作用の影響を受けずに動ける領域についての特徴的な長さに対応した物理量である．図4と図5に１成分系と２成分系における無次元化された平均自由行程の結果を示す．横軸は無次元化された逆温度である．

**図4:**１成分系における平均自由行程

**図5:**２成分系における平均自由行程

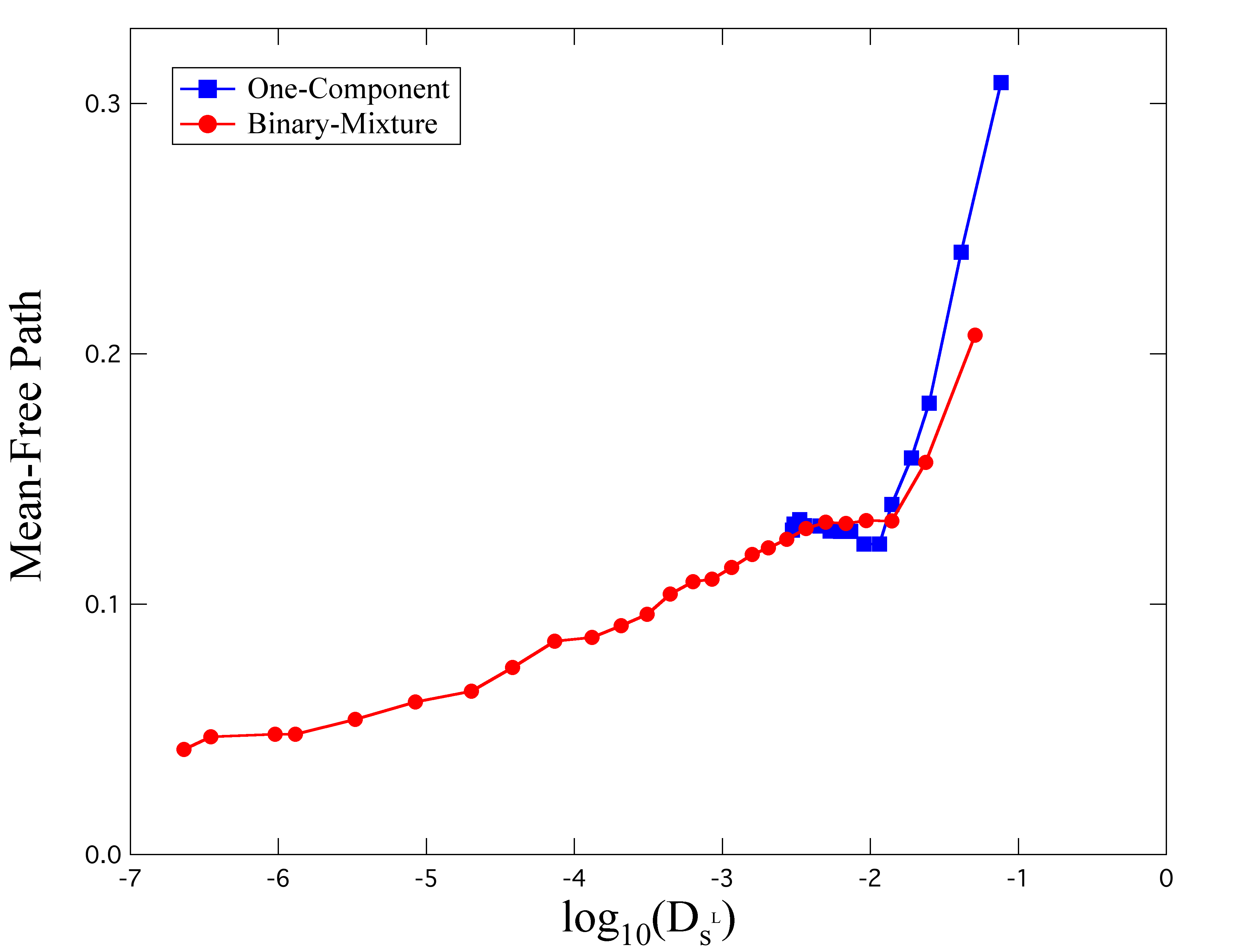
１成分系も２成分系も高温領域においては平均自由行程が急激に減少し，その後ほぼ一定になる．１成分系では結晶化が起こるために低温領域の自由長は測定できない．２成分系における低温領域では，温度が下がる（逆温度が上がる）につれて緩やかに減少していく．徳山は，長時間自己拡散係数と平均自由行程の関係はシステムに依存しない普遍的なものであるということを提案している[3,4]．そこで，図6に１成分系と２成分系についての長時間自己拡散係数と平均自由行程との関係を示す．ただし，数密度の違いを考慮して，１成分系の自由長は20.89/23.00倍だけスケールされている．このように，数密度が等しければ長時間自己拡散係数と平均自由行程の関係は１成分系と２成分系で同じものとなる．