A.　研究目標

上で示されるようにガラスは工学的・工業的によく使われている物質の一つである。最近の科学技術の発達により液体―ガラス転移のダイナミクスは、実験・計算機実験により精力的に研究されている。しかし、液体からどのようにしてガラスになるのかの詳細は明らかにされず、本質的理解には程遠いのが現状である。そこで本研究では、複雑液体のひとつである中性コロイド分散系について、コロイド分散系を模擬するブラウン動力学法を用いて流体の空間構造と緩和機構を詳細に解析し、この複雑な問題の解決の糸口を見い出す。また、比較のために、原子・分子系を模擬する分子動力学法による研究も行う。

B.　研究内容

　近年、液体−ガラス転移現象は通常のガラス形成物質に限らず、中性コロイド分散系（液体の中に直径が10nmから1μmの大きさの粒子が分散している系）でも確認されることが報告された。通常のコロイド粒子は、電荷を持っている。一方、中性コロイド分散系は、poly-(12-hydroxy stearic acid):(PHSA)の薄い層を持つ、電荷を持たない中性コロイド粒子poly-(methyl methacrylate):(PMMA)が分散している系である。そのため、コロイド粒子は、電荷を持たないため、剛体球としての振舞いをする。また、粒子の大きさは、直径=100(nm)程度であり、原子・分子(1.0Å程度)より大きい。そのため、光散乱、X線散乱、光学顕微鏡、また共焦点顕微鏡などの簡素な実験装置で、コロイド分散系の平均構造・粒子運動・局所的構造、そして動的性質などが観察することができるという長所がある。

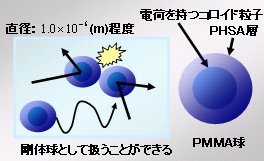図1　コロイド粒子

　ガラス形成物質は、温度を急冷することで過冷却状態を経てガラス状態になる。それとは別に、コロイド分散系では体積比φ（粒子全体の体積／系全体の体積）を変化させることで、ガラス状態を作り出せることができる（下の図参照）。コロイド液体の温度・圧力を一定にし、粒子の体積比を増加させると過冷却コロイド液体状態(0.545 ≦φ＜ 0.580)になり、更に増加させていくとコロイドガラス状態(φ≧0.58)になる。液体−ガラス転移点近傍において、コロイド液体は体積比を増加させると拡散係数は非常に小さくなる。一方、ガラス形成物質は、温度を下げていくと粘性係数は異常に増加する。このように両者の振舞いは、定性的に非常によく似通っている。また、コロイド分散系は、必ずしもコロイドガラスになるとは限らず、外乱やコロイド粒子半径の分散度との兼ね合いで、結晶の配列を示すコロイド結晶を形成する。つまり、凝固体積比φ=0.494、融解体積比φ=0.545の固相−液相転移も存在する系であり、工学的に興味深い相変化や相転移現象といった種々様々の面白い過程の現象を兼ね備えている系でもある。 そこで、中性コロイド分散系で起こる現象を理解することによって、液体―ガラス転移現象に対する、本質的な理解、一般的理論を構築する糸口を見出されることが期待されている。

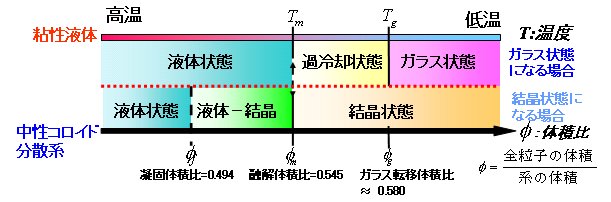図2　粘性液体と中性コロイド分散系での比較

　このようなことから、中性コロイド分散系の計算機実験に関する研究が多く行われてきている。中性コロイド分散系のシミュレーションとして、コロイド分散系を模擬するブラウン動力学法が用いられている。ブラウン動力学法では、コロイド粒子(剛体球粒子)を、溶媒分子の熱運動の寄与である揺動力を用いたLangevin方程式に従いブラウン運動させる。中性コロイド分散系には、コロイド粒子と溶媒間での相互作用と、コロイド粒子間での相互作用がある。後者はその中でも、二種類の相互作用が存在すると考えられている。すなわち、�@お互いが衝突することによる直接的相互作用および、�A時間と共に液体を通して及ぼし合う流体力学的相互作用である（下図の赤線）。その流体力学的相互作用は、高濃度領域(コロイド過冷却液体・ガラス状態形成)においてに重要な機構であると報告されているが、数値的に解くことが困難なため本計算ではその作用を考慮せず計算をする。また、比較のため、真空中に剛体球が存在する原子分子系での計算も行う。原子分子系を模擬する分子動力学法では、剛体球粒子はニュートン方程式に従い運動する。

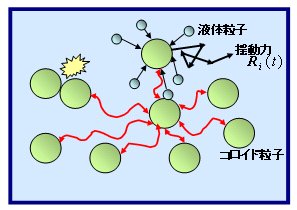図3　分散媒中のコロイド粒子に働く相互作用

C.　研究成果

　図４、５に、すべて同じ大きさの粒子10976個の系での、コロイド分散系と原子分子系での液体状態と結晶状態の平均二乗変位と動径分布関数を示す。図中の青線は結晶状態からクエンチした初期配置から、赤線は液体状態からクエンチした初期配置から計算を行った結果を表す。平均二乗変位Ｍ２(t)は、粒子が時間tの間に元の位置からどれだけ移動したか、その目安となる量であり、移動変位の二乗の平均した量である。一方、動径分布関数g(r)とは、ある粒子iを中心として距離rに存在する確率数密度分布であり、系の構造の特徴を表すことができる。そこで、平衡状態に達した時のそれぞれの動径分布関数を示す。

コロイド分散系、原子分子系ともに、結晶状態では、平衡状態に達すると、平均二乗変位が一定値となる。また、動径分布関数も面心立法格子上に粒子が配置したときに見られる特徴的なピークを持つ。一方、液体状態では、平均二乗変位は長時間たつとｔ^１（拡散過程を示す）に比例して増大し、動径分布関数は1近傍で揺らぐのみとなる。

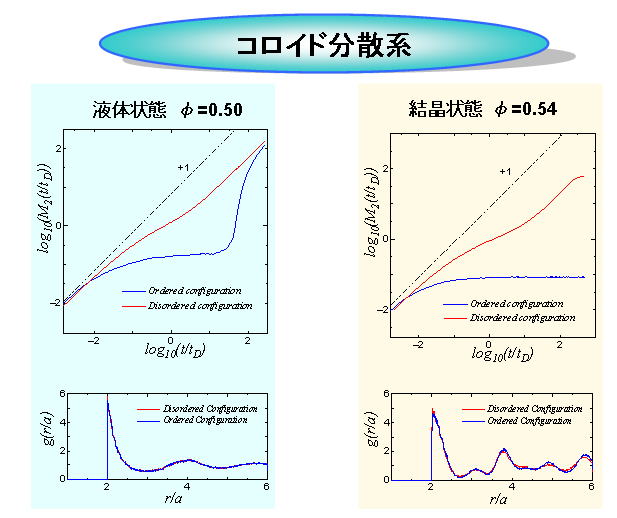
図４　コロイド分散系の平均二乗変位と動径分布関数（液体状態と結晶状態）

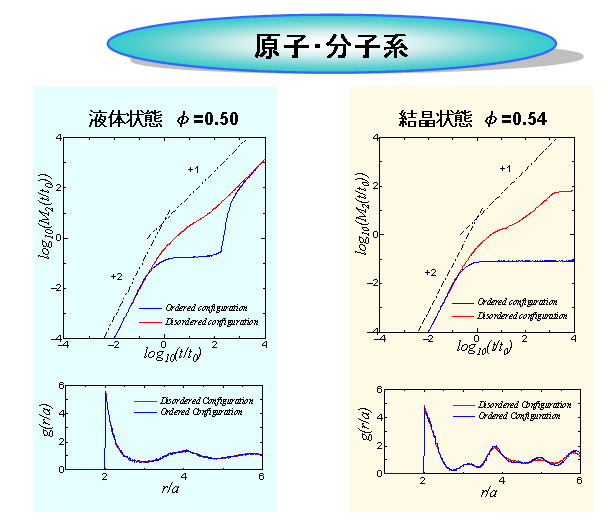図５　原子分子系の平均二乗変位と動径分布関数（液体状態と結晶状態）

平成１４年度修了生