研究成果

航空機・宇宙機の設計開発においては、機体の試作や試験に伴う時間的および経済的な制約が大きいことから、試験の代替や性能の予測のために数値シミュレーションが頻繁に利用されている。これにより、機体設計に大きく影響する物理現象を正確かつ忠実に再現・評価し、その結果を実際の設計開発にフィードバックして高い信頼性を確立することが期待されている。
本研究では、無数の不確かな物理要因によって生み出される実世界に近い物理現象を定量的に評価するための数値シミュレーション手法の開発に着手した。この種の数値シミュレーションを単純なサンプリング解法(例えばMonte Carlo法)によって行おうとすると、非現実的で膨大な計算コストが要求される。よって昨今では、近似解法(例えば多項式カオス展開法:PCE法)の利用が主流となっているが、近似精度を上げようとして近似次数を上げると、推定される解の応答の中に非物理的な振動が発生するという逆効果が見られた(図1a)(図1b)。そこで本研究では、Kriging理論に基づき解析空間を確率・統計論的にモデル化し、さらに離散誤差理論に基づき解析空間内で予想される重要な情報(感度、不確定性など)を定量的かつ動的に抽出するアルゴリズムを構築した。これを新たな近似解法として数値シミュレーションに組み込むことで、精度・効率・ロバスト性の改善を図った。これまでに、解析空間の次元数および連続性の異なる数々のテスト問題に対して新解法を適用した結果、推定される解の応答の安定化(図2)および解の統計量に含まれる誤差の低減(図3)を、すべての適用問題において確認した。今後はこの新解法を応用して、変動気流下での航空機の空力性能予測や最適設計など、より現実的な工学事例での物理現象の定量化および設計の高信頼性化を目指す。
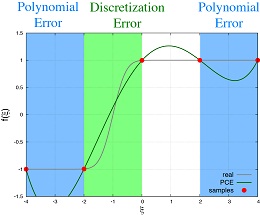 図1a 従来解法(PCE法)によって推定された解の応答(4次精度) |
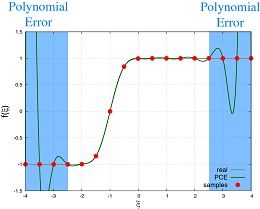 図1b 従来解法(PCE法)によって推定された解の応答(16次精度) |
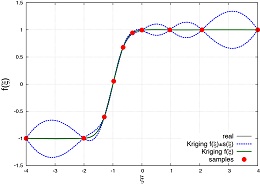 図2 新解法(Kriging+離散誤差理論)によって推定された解の応答 |
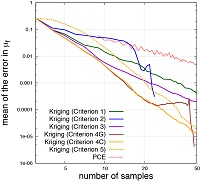 図3 従来解法(PCE法)および新解法(Kriging+離散誤差理論)によって推定された解の統計量に含まれる誤差 |
学術論文
-
Koji Shimoyama, Soshi Kawai, and Juan J. Alonso, Dynamic Adaptive Sampling Based on Kriging Surrogate Models for Efficient Uncertainty Quantification, to be submitted.
学会発表
- Koji Shimoyama, Soshi Kawai, and Juan J. Alonso, Dynamic Adaptive Sampling Based on Kriging Surrogate Models for Efficient Uncertainty Quantification, 15th AIAA Non-Deterministic Approaches Conference, (2013), AIAA 2013-1470.