A.　研究目標

ガラスは人類とは切っても切れない関係にある．今から5000年ほど前に偶然にして初めて精製されたとされるガラスは長い時を経た今でも重要な材料として用いられている[1]．

通常，液体を融点以下の温度に冷却すると結晶となる．しかし，急冷や混合といった特殊な条件により結晶化を避けつつ冷却すれば過冷却液体，さらに冷却するとガラスとなる．ここでいうガラスとは粘性が非常に強いためにほとんど流動していないように見える流体を表し，日常生活で用いる概念とは異なる．工学的には粘性率が10の13乗ポワズを超える流体をガラスと定義している．室温におけるマヨネーズの粘性率が10程度であることを考えると，ガラスは実用的な時間スケールでは固体として扱えるくらいに粘性の大きい流体である．しかしながら実際は長い時間をかけて流動している．

ガラス物性の工学的研究が非常に進んでいるのに対して，ガラス転移メカニズムの物理的解明は未だ完全にはなされていない．近年は大規模なシミュレーションも行われており，これまでになされた膨大な実験データと合わせて，理論的解明に向けての気運が高まっている[2]．ガラスの更なる応用の可能性のためにも，転移メカニズムの解明は必要不可欠である．

本研究では過冷却液体やガラス転移現象の動的なメカニズムの解明を目標としている．研究手法としては統計物理学的方法論とシミュレーションを用いる．現段階では分子動力学シミュレーションによる研究を主に行っており，Kobらによる研究[3]を参考にしている．これは２種類の粒子が混ざり合った状態でのシミュレーションである．２成分という特殊な条件により結晶化を避けて過冷却液体状態を作ることに成功している．しかし，この系はたとえ１成分であっても結晶とはなり得ないように数密度や粒子数が調整された特殊な系である．

本研究でも２成分とすることで過冷却液体やガラス状態の再現を目指すのであるが，１成分系では液体-結晶相転移が起きるような系についてシミュレーションを行う．

B.　研究成果

　(1)１成分系における液体結晶相転移

１成分系の分子動力学シミュレーションにより得られた結果を示す．無次元化された温度をパラメータとして測定した無次元化された圧力を図1に示す．

図1: 各温度での圧力の値

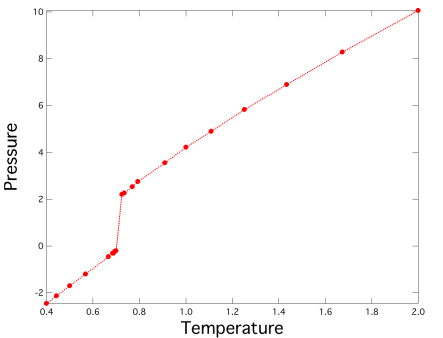
このように示強性変数である圧力に跳びが見られることから何らかの相転移が起こっている．

また，T=0.725とT=0.699についての動径分布関数は図2，図3がそれぞれ得られた．横軸の長さについては無次元化されている．

図2: T=0.725における動径分布関数

図3: T=0.699における動径分布関数

T=0.725における動径分布関数は短距離秩序しかなく，長距離での秩序は見られない．一方，T=0.699では長距離秩序が見られる．以上のことをあわせると，T=0.725とT=0.699の間で液体-結晶相転移が起こっていることが分かる．

融点をさらに精度良く定めようと計算を行っているが，転移点近傍では平衡状態に至るまでの時間が非常に長いために信頼できる結果を得るには至っていない．

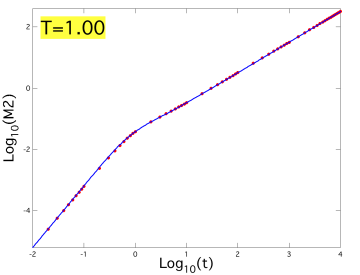
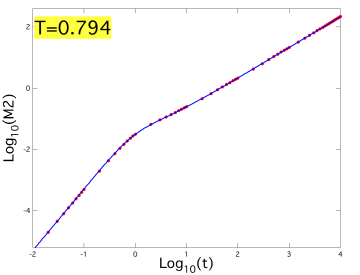
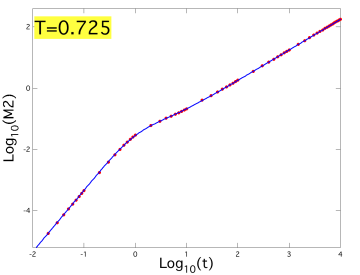
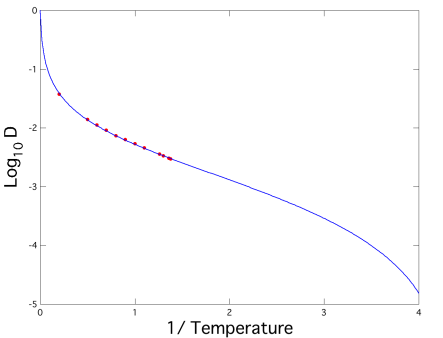
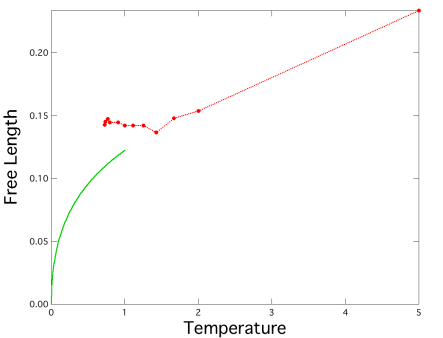
液体領域について，分子場理論[4,参照HP]による平均二乗変位の解析結果を図4，図5，図6にそれぞれ示す．また，分子場理論による無次元化された長時間拡散係数の解析結果を図7に，無次元化された温度と自由長の関係を図8にそれぞれ示す．シミュレーションによって得られた値は赤い点もしくは赤い破線で表し，分子場理論による理論線は青色の実線で描かれている．また，自由長の図における緑色の実線は結晶における自由長を理論的に求めたものである．

図4: T=1.00における平均二乗変位

図5: T=0.793における平均二乗変位

図6: T=0.725における平均二乗変位

図7: 無次元化された温度の逆数と長時間拡散係数の関係

図8: 無次元化された温度と自由長の関係

　(2)２成分系における過冷却液体状態の実現

　[under construction]

参考文献

1

P. G. Debenedetti and F. H. Stillinger, Nature, 410 (2001), 259-267.

2

M. D. Ediger, C. A. Angell, and S. R. Nagel, J. Phys. Chem., 100 (1996), 13200-13212.

3

W Kob, J. Phys. Condens. Matter, 11 (1999), R85-R115.

4

M Tokuyama, Physica A, 364 (2006), 23-62.