Complex Flow Research Division
Computational Fluid Physics Laboratory

ProfessorYuji Hattori

Associate ProfessorMakoto Hirota
Flow phenomena are ubiquitous in many areas ranging from biological to astronomical scale and in many applications including aerospace engineering, environmental studies and energy technologies of next generation. Thanks to the rapid growth of computational power, computer simulation of flow phenomena has acquired a wide range of application. There are increasing needs for highly accurate simulation as well as novel methods for obtaining useful knowledge from huge data. In our laboratory, we are studying flow phenomena by numerical simulation. New methods for numerical simulation and their application are developed. We are also doing theoretical studies of fluid dynamics by mathematical approach.
Direct Numerical Simulation of Complex Flow Phenomena
We study complex flow phenomena by direct numerical simulation. In particular turbulent flows are investigated using highly-accurate numerical methods in order to understand the statistical properties of turbulence and develop accurate turbulence models.
-
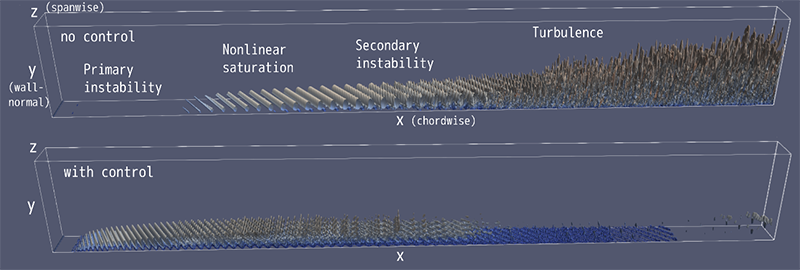 Suppression of turbulent transition of boundary layer by roughness element
Suppression of turbulent transition of boundary layer by roughness element Vortices in homogeneous isotropic turbulence
Vortices in homogeneous isotropic turbulence
Development of Highly-Accurate Method for Numerical Simulation of Complex Flow Phenomena
The flows in nature and engineering often involve complex bodies which move and/or deform in the flow regions. We develop numerical methods for highly-accurate numerical simulation of the complex flow phenomena. Using the methods we also perform realistic direct numerical simulation of various flow phenomena.
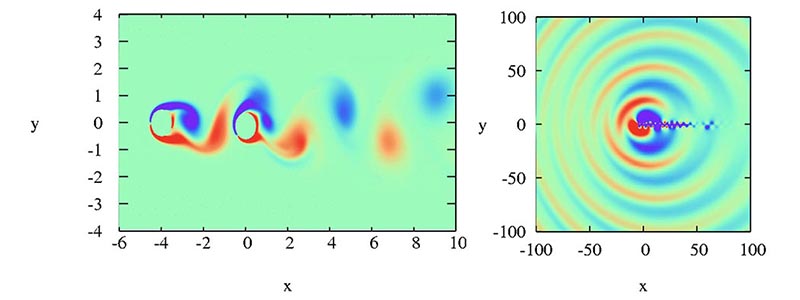 Results of simulation by corrected volume penalization method. Flow past an oscillating cylinder and a fixed cylinder. (Left) vorticity field, (right) sound pressure field.
Results of simulation by corrected volume penalization method. Flow past an oscillating cylinder and a fixed cylinder. (Left) vorticity field, (right) sound pressure field.
Vortex Dynamics and Applied Mathematical Fluid Dynamics
It is important to understand the vortex dynamics in investigating flow phenomena. The fundamental properties and the dynamics of various vortical structures are studied. Our goal is to reveal the characteristics, universality of the vortical structures from the viewpoint of vortex dynamics. Fundamental and general methods are important in the research of fluid science. Various tools in mathematical physics, especially in differential geometry, functional analysis, dynamical system etc. are developed and applied for fluid science.
-
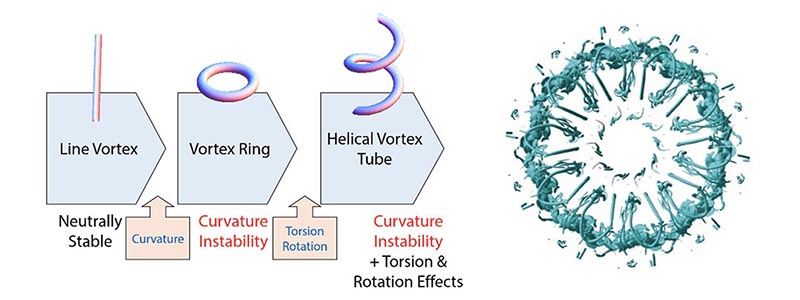 Theory of curvature instability and destabilized vortex ring
Theory of curvature instability and destabilized vortex ring
